Stavo riflettendo a quanto sia importante nella cultura egizia il quadrilungo (o rettangolo 1-2) ovvero un rettangolo in cui il lato lungo è il doppio di quello corto.
Si tratta in effetti di due quadrati uguali con un lato in comune.
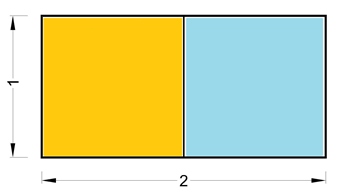
Quadrilungo o Rettangolo 1-2
Abbiamo già avuto modo di vedere quante volte gli Egizi abbiano usato questa figura geometrica per i più svariati impieghi il più famoso dei quali è certamente la pianta (ovvero il pavimento) della camera del re all’interno della Grande Piramide. E se lo usarono per un luogo sacro e immensamente importante per loro, doveva esserci una fortissima motivazione.
È cosa nota che tracciando le due diagonali di un quadrilungo i cui lati misurino 1 e 2, esse valgono 2,236. Lo si deduce facilmente applicando il teorema di Pitagora. [1]
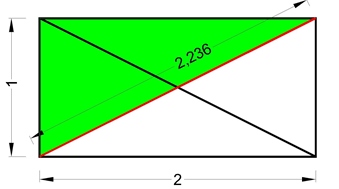
Quadrilungo e le sue diagonali
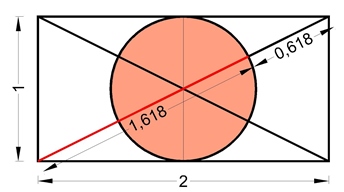
Diagonali in rapporto aureo tra loro
È altrettanto noto che tracciando al centro del rettangolo un cerchio con diametro uguale al lato corto (in questo caso = 1), esso divide le diagonali in due parti che sono in rapporto aureo tra di loro. ([2])La parte rossa della diagonale vale 1,618 (ovvero il numero aureo il cui simbolo è Ф), mentre la parte restante = 0,618 è l’inverso del numero aureo.
Ovviamente è possibile fare lo stesso ragionamento anche per l’altra diagonale. Ed è proprio per questo che, mentre osservavo il disegno nel suo insieme, mi sono chiesto cosa succederebbe se tracciassi due archi di cerchio usando come raggi le parti auree delle due diagonali. Quelle in rosso e blu della figura seguente.
Ciò che ne esce, sembra il profilo di un arco ogivale tanto usato nell’architettura gotica.
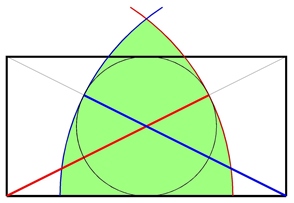
Doppie diagonali + archi
Però continuavo a pensare che ci fosse anche dell’altro e ad un certo punto “l’ho visto”.
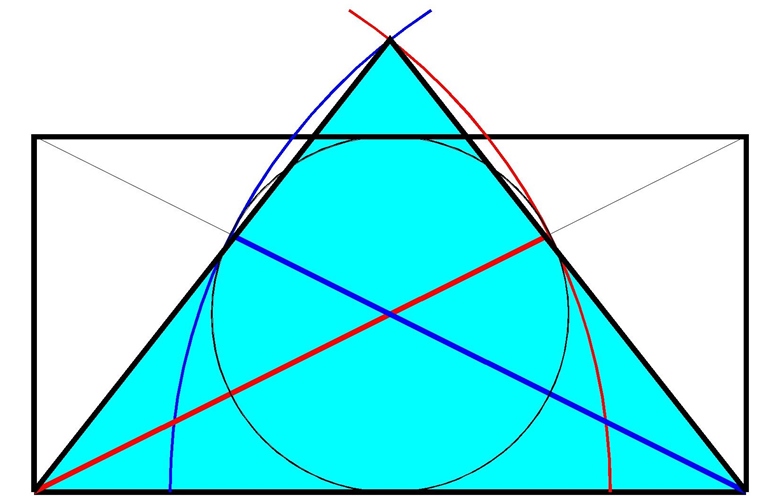
Profilo Grande Piramide
Infatti collegando il punto di incontro dei due archi con la base del quadrilungo, ottenevo un profilo a me ben noto, familiare direi… Il profilo della Grande Piramide di Giza.
Non voglio annoiare il lettore con noiosi calcoli matematici, però posso concludere che a verifica matematica fatta, la mia intuizione è confermata numericamente con uno scostamento percentuale pari solo allo 0,03%. Quindi un preciso rapporto tra la sezione della Grande Piramide e un quadrilungo, esiste. Lo scostamento seppur minimo dipende dal fatto che il numero aureo è irrazionale…
[1] – Per il Teorema di Pitagora: 1² = 1, mentre 2² = 4 quindi 1+ 4= 5 la cui radice = 2,236.
[2] – Infatti 1,618 : 0,618 = 2,618 che è il quadrato del numero aureo.




